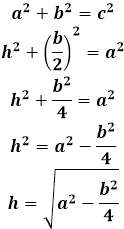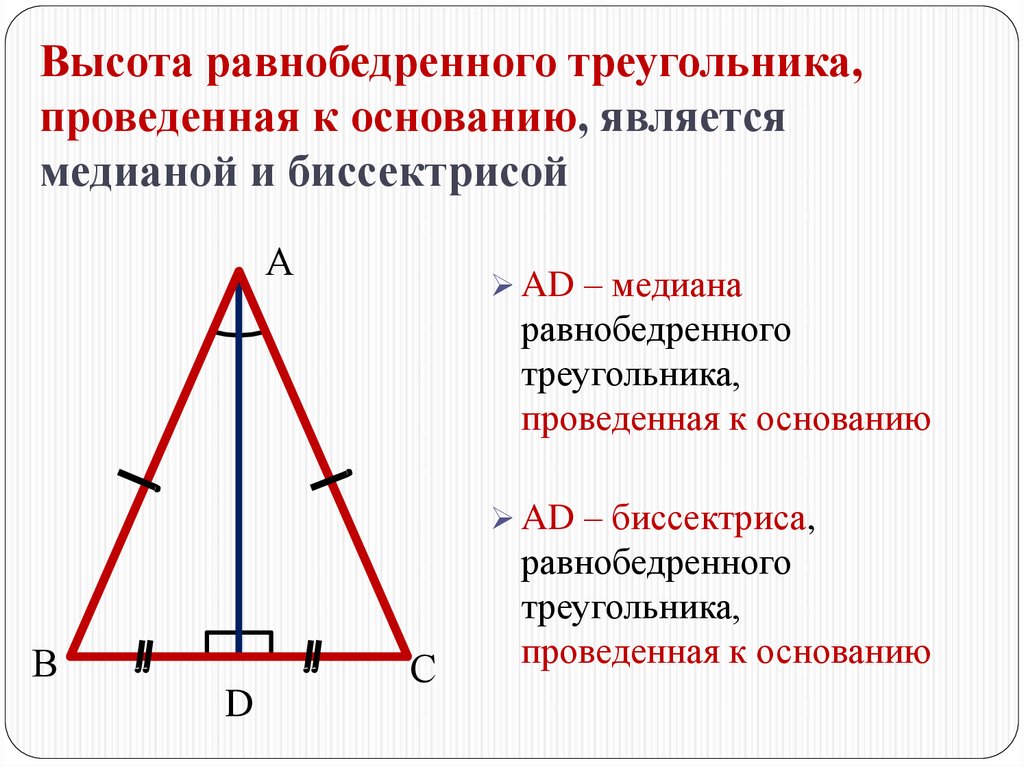
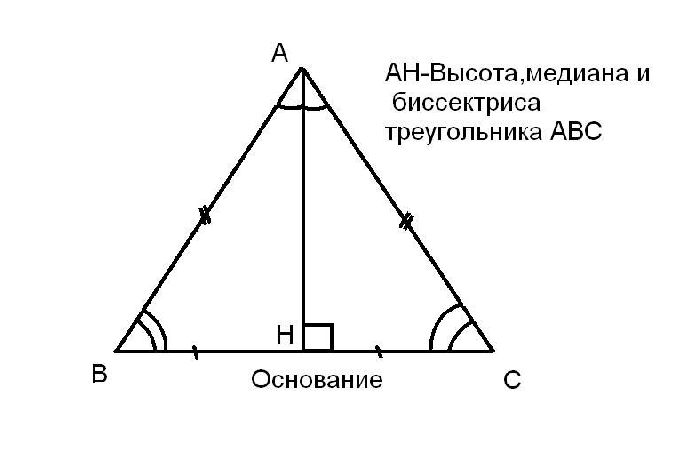
Свойства высоты равнобедренного треугольника
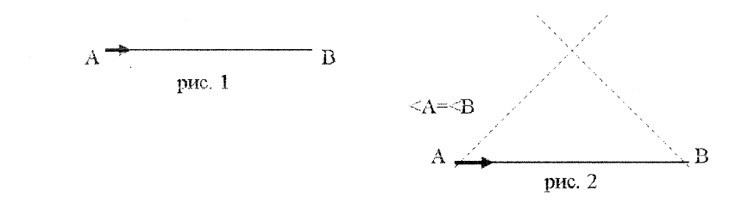
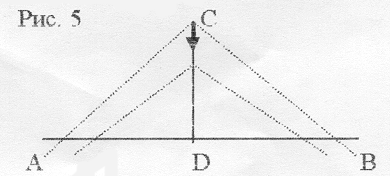
Черепашка нарисовала горизонтальный отрезок АВ. Вернулась в точку А и смотрит в направлении на восток рис. Достройте этот отрезок до треугольника так, чтобы углы при основании АВ были равны рис. Задание 1: Исследуйте длины получившихся сторон. Задание 2 : Постройте еще несколько треугольников с другими величинами углов при основании АВ.







Регистрация Вход. Вопросы - лидеры. Помогите решить черчение 1 ставка.
- Содержание
- Задачи: - обучающие: закрепить знания о медиане, биссектрисе, высоте, равнобедренном треугольнике; создать условия для усвоения знаний о свойствах равнобедренного треугольника; сформулировать и доказать свойство биссектрисы равнобедренного треугольника; научить применять данное свойство при решении геометрических задач. Тип урока: Урок изучения нового и первичного закрепления.
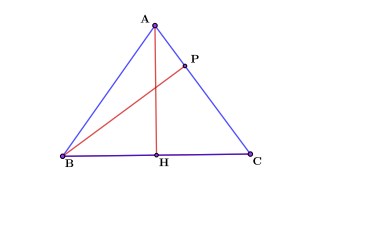
- Иногда медианой называют также прямую , содержащую этот отрезок, а иногда длину этого отрезка.
- Цель учителя : Создать условия для введения понятий равнобедренного треугольника, равностороннего треугольника, рассмотрения свойств равнобедренного треугольника и демонстрации их применения на практике. Личностные результаты : формирование готовности и способности обучающихся развиваться на основе мотивации к обучению и познанию, проявляют познавательный интерес к изучению предмета.










| 282 | О проекте. О нас пишут. | |
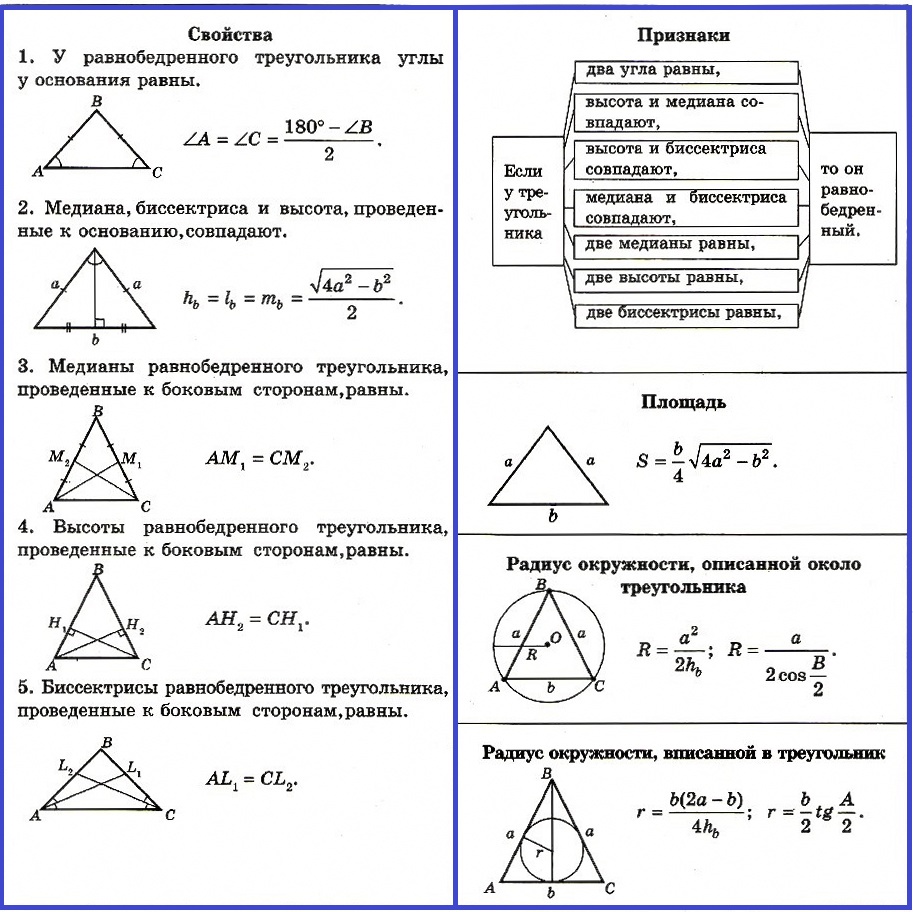
| 266 | Для повторения мы выбрали эти темы. Приводить доказательство теорем, содержащихся в учебнике, не будем, лишь напомним основные теоремы. | |
| 465 | Программа предназначена для расчета высоты произвольного равнобедренного треугольника. Треугольником является многоугольник, который имеет три вершины и три стороны. |
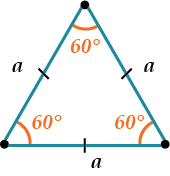
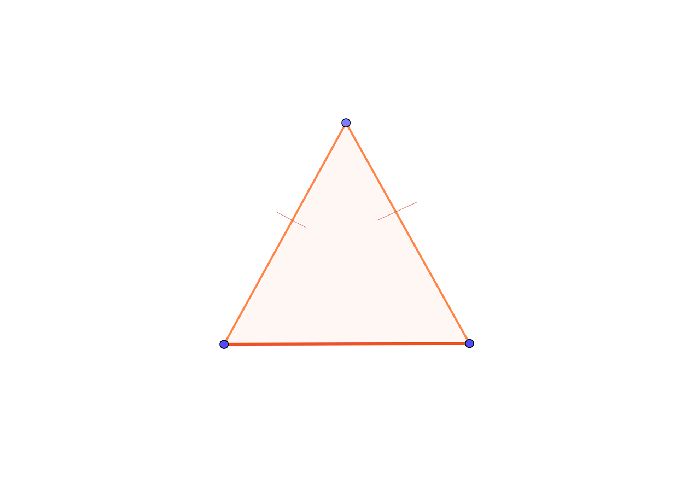
В равнобедренном треугольнике прекрасно всё: и три угла, и два симметричных бедра. Полюбуемся этой фигурой, а заодно узнаем ее свойства, признаки и формулы, чтобы решать задачки легко. Равнобедренный треугольник — это треугольник, в котором две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
.png)