Вы точно человек?
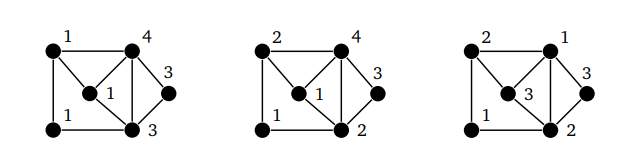
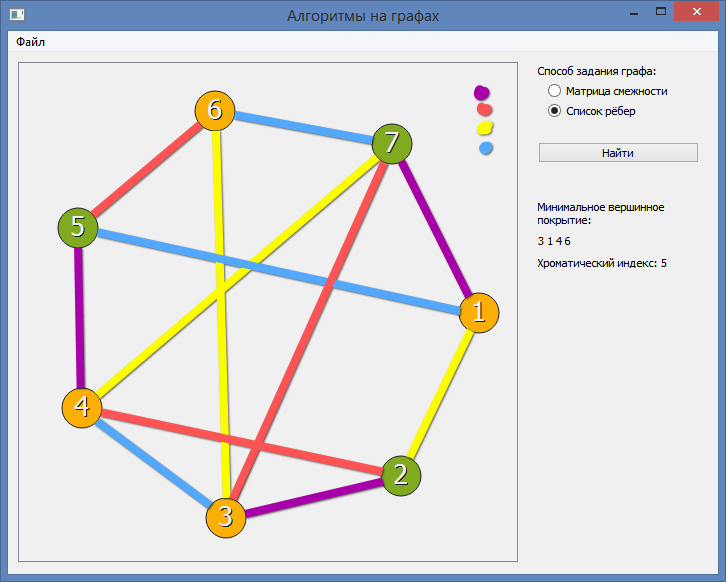
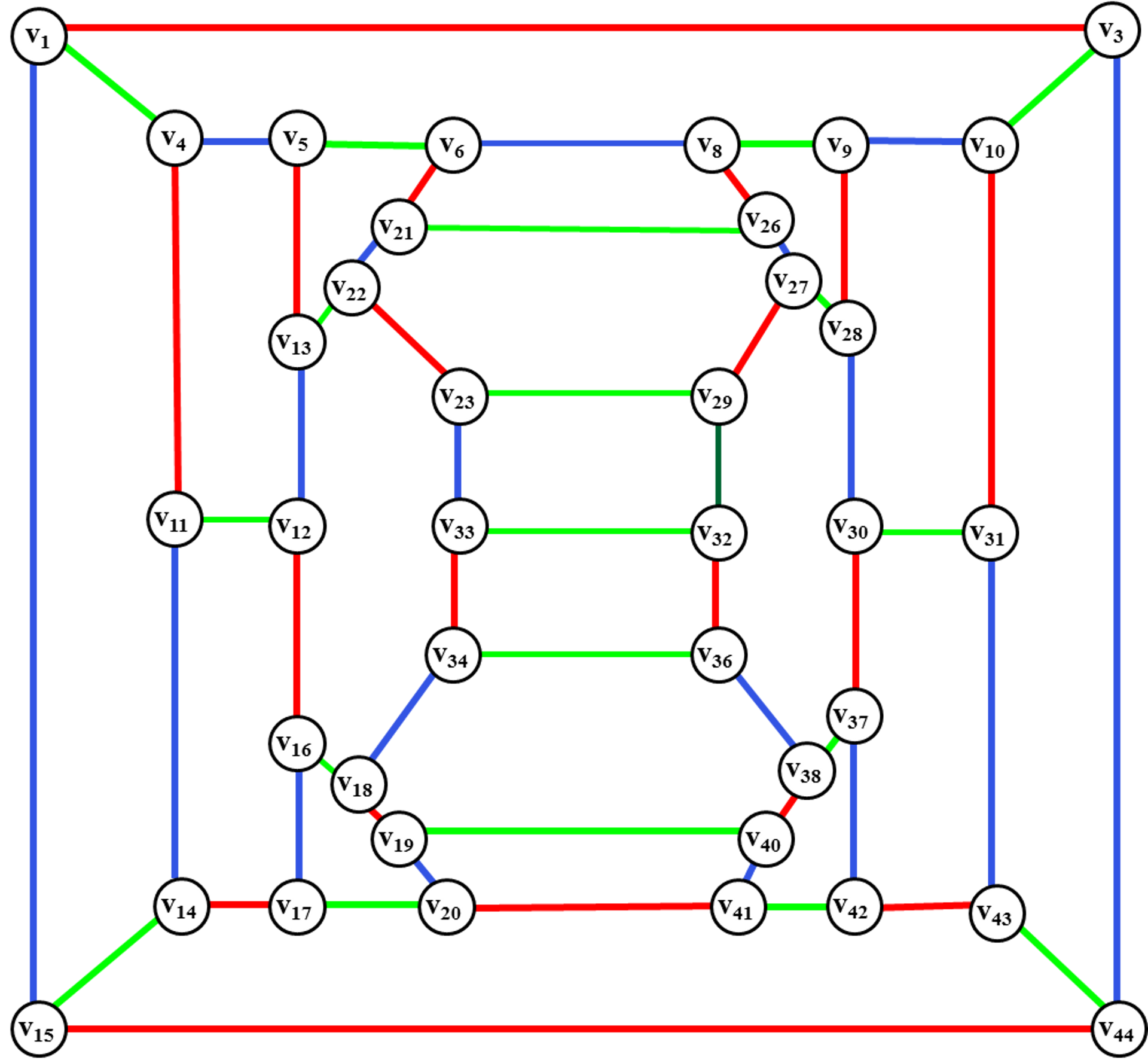
В этой записи я решил представить алгоритм, придуманный мной под впечатлением от распределённых distributed алгоритмов. Алгоритм строит субоптимальную правильную вершинную раскраску неориентированного графа. Алгоритм довольно прост и, возможно, был в том или ином виде представлен в литературе. Под конфликтами понимается наличие одинаково окрашенных вершин-соседей. Если вершину v перекрасить в цвет c , то конфликт будет разрешён при условии сохранения прежних цветов соседями v.
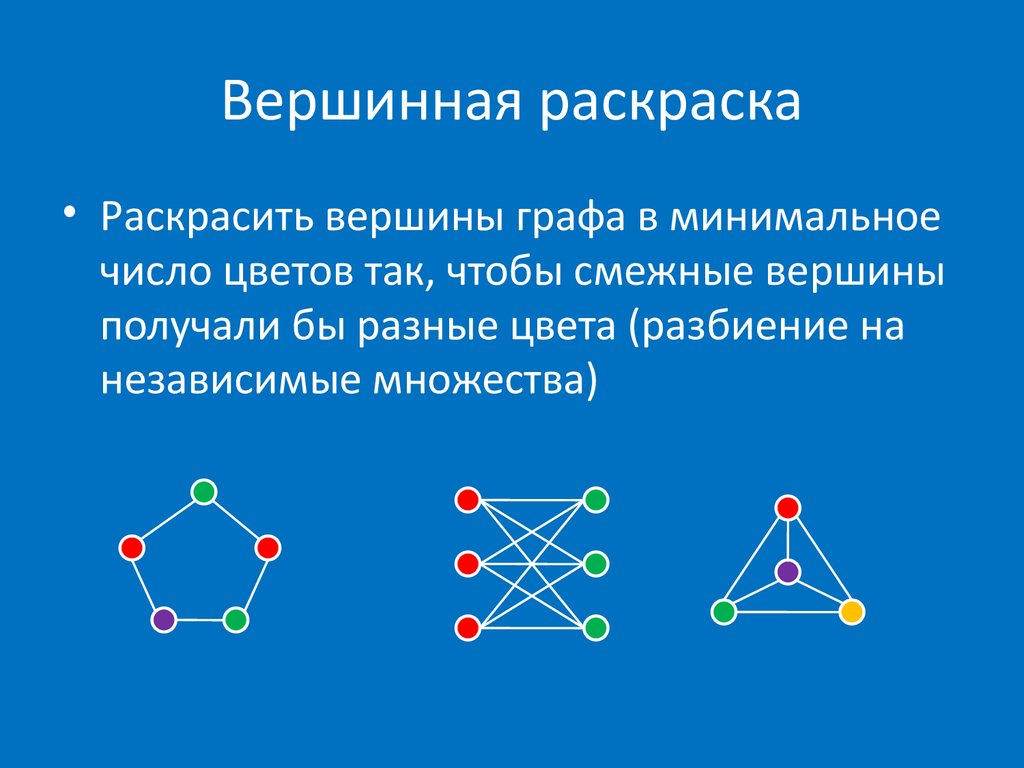






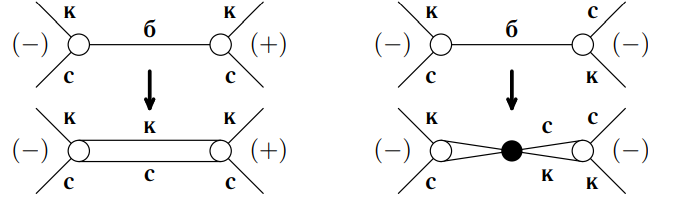
Раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета - это числа. Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения в множестве.
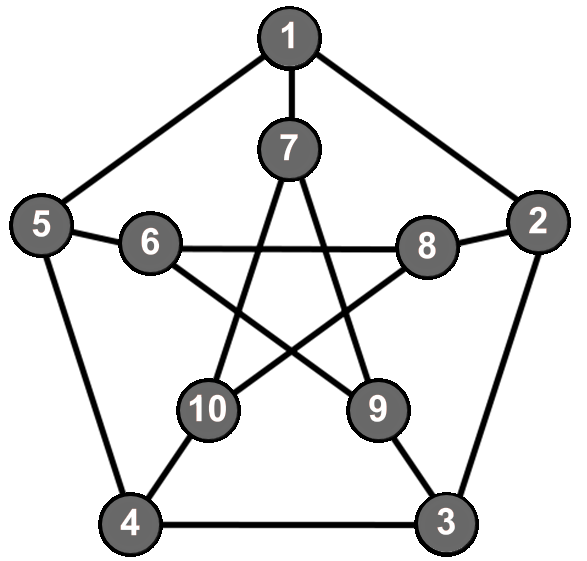

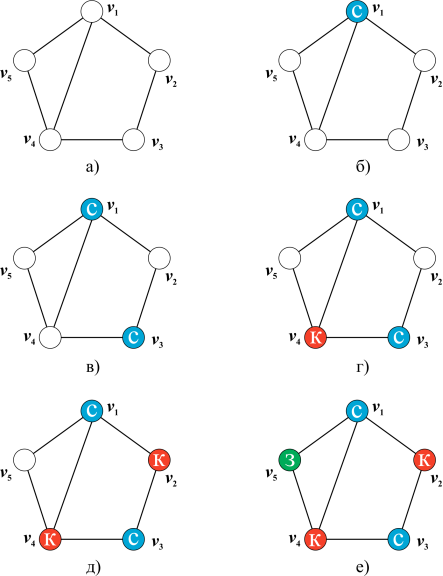


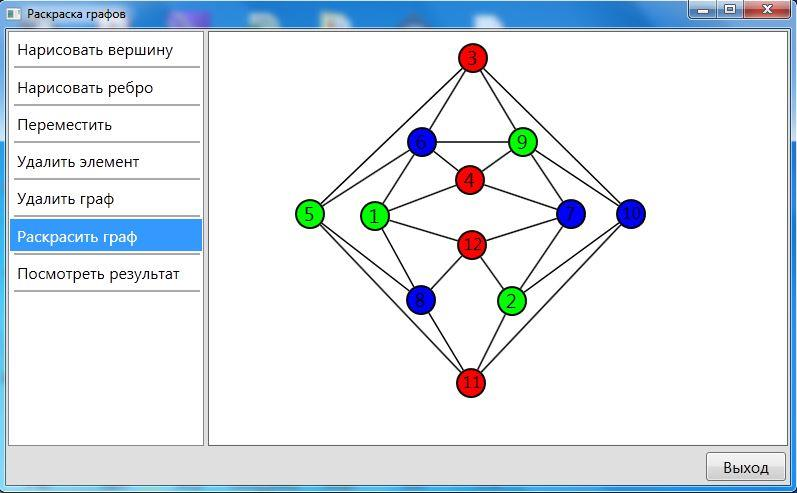
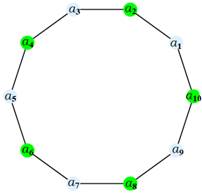
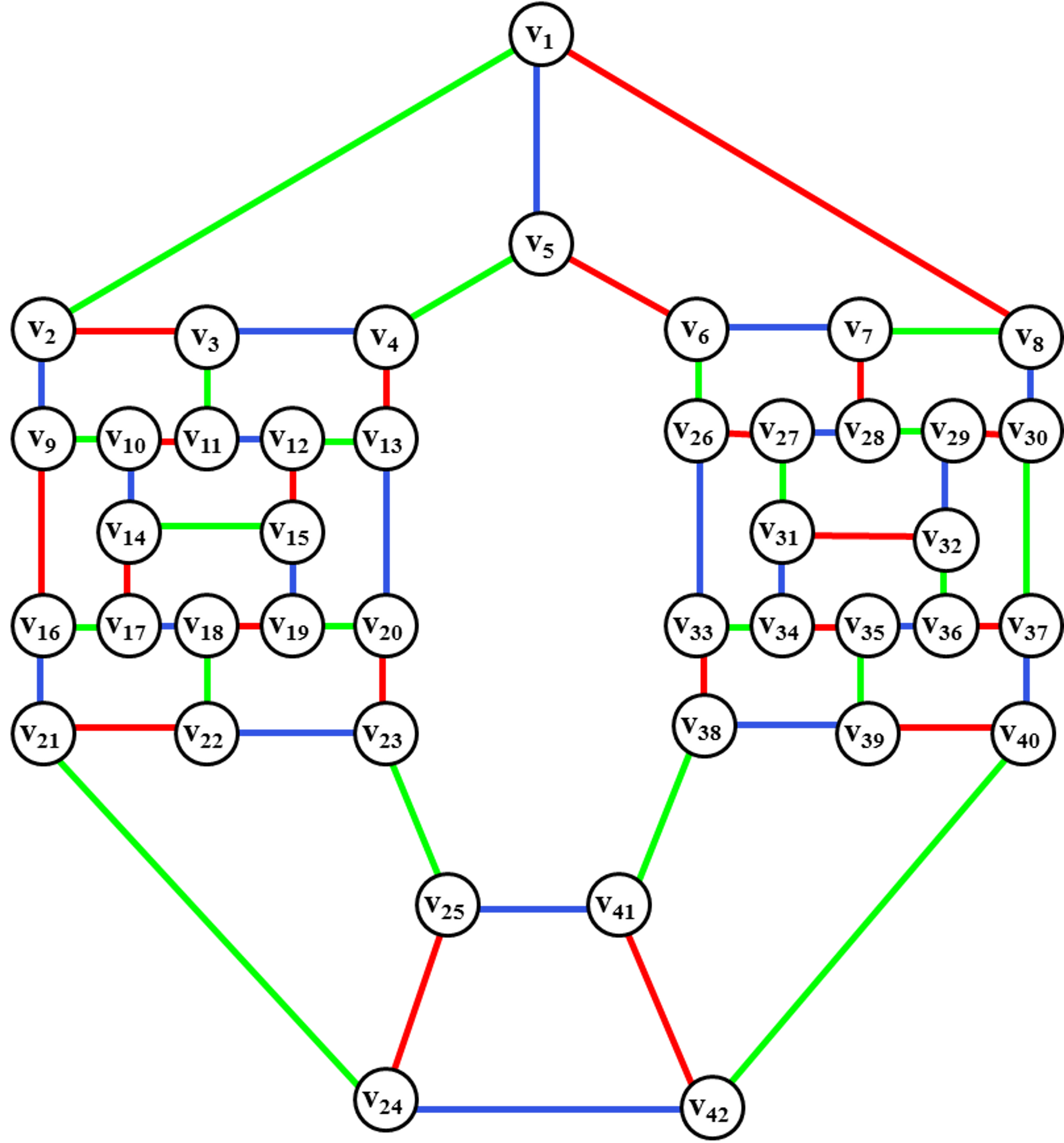
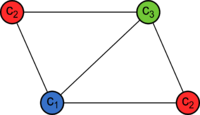
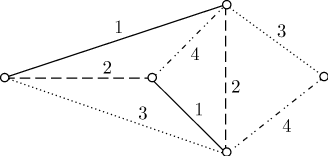
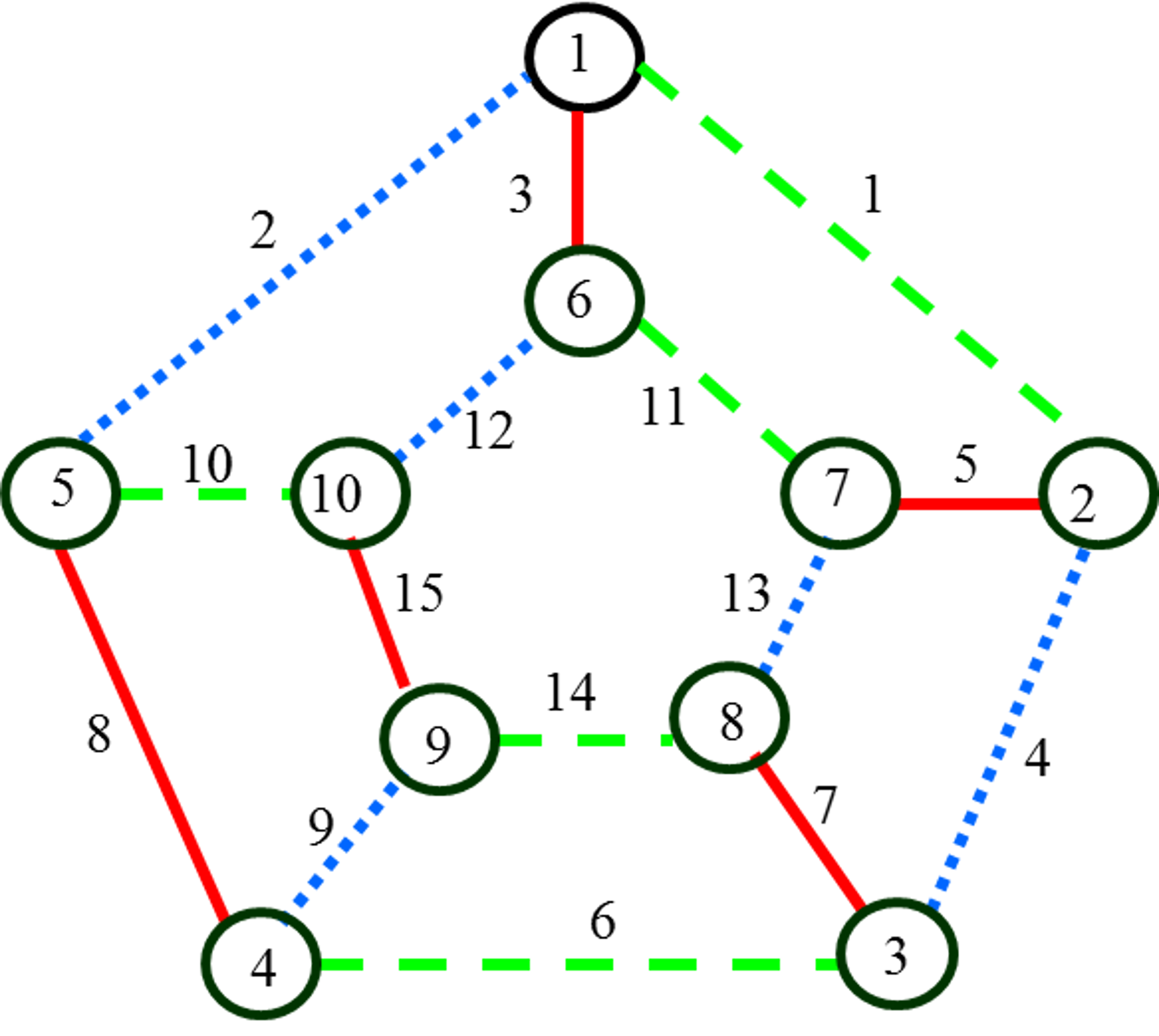



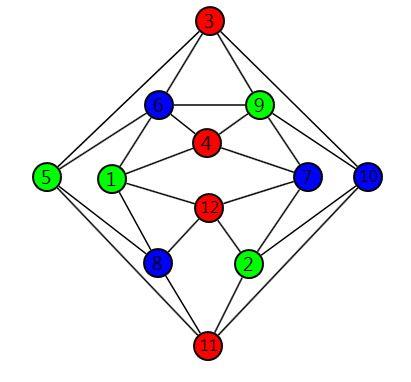
При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число. В теории графов подобные задачи формулируются в терминах раскраски вершин графа.